A myriad of mechanical and electrical specifications must be considered when selecting the best connector system for your design. An incomplete, first-pass list of considerations include the type of termination, available footprint space, processing and operating temperature and humidity ranges, shock and vibration requirements, ROHS-compliant/lead-free standards, packaging, and non-signal voltage and current requirements, just to name a few.
Can you identify one big consideration that I intentionally left off the list? If you guessed mating and unmating forces (insertion and withdrawal forces of the mated connector set) then you are either very perceptive or you read the title of this blog. Either way, the mating and unmating forces of the connector set are critical to its success. Designers need to strike the right balance of insertion and withdrawal forces (so they can mate and un-mate the boards and not damage them or the connectors in the process), and achieve sufficient normal forces for a reliable connection.
Kevin Meredith, a Product Engineer at Samtec, prepared a paper on “Calculating Mating and Un-Mating Forces For Samtec Connectors.” This paper examines the mechanics of of mating forces at the individual contact level.
Per Kevin, the mating and un-mating force for Samtec connectors can vary dramatcially depending on the connector type and pitch. The mating force is a function of the contact geometry, the contact spring rate, and the coefficient of friction. To better understand these forces at the connector level we will examine what goes on at the individual contact level. In most cases it is not necessary for Samtec customers to perform these calculations as Samtec tests the smallest, largest and middle pin count connectors during the product qualification process.
For single and twin beam contact style connectors calculating the mating force is fairly straight forward. You just multiply the peak force per circuit times the number of circuits. This is an idealized approach as it does not take into account plastic binding from misalignment but is useful for sizing injectors, extractors, or similar hardware in the event test data is not available.
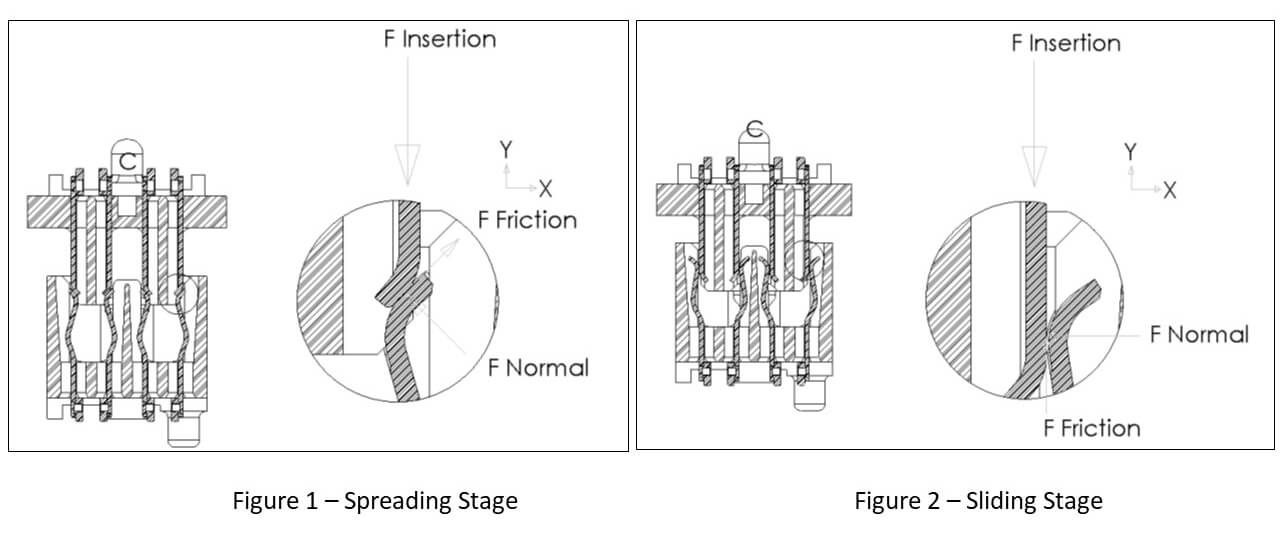
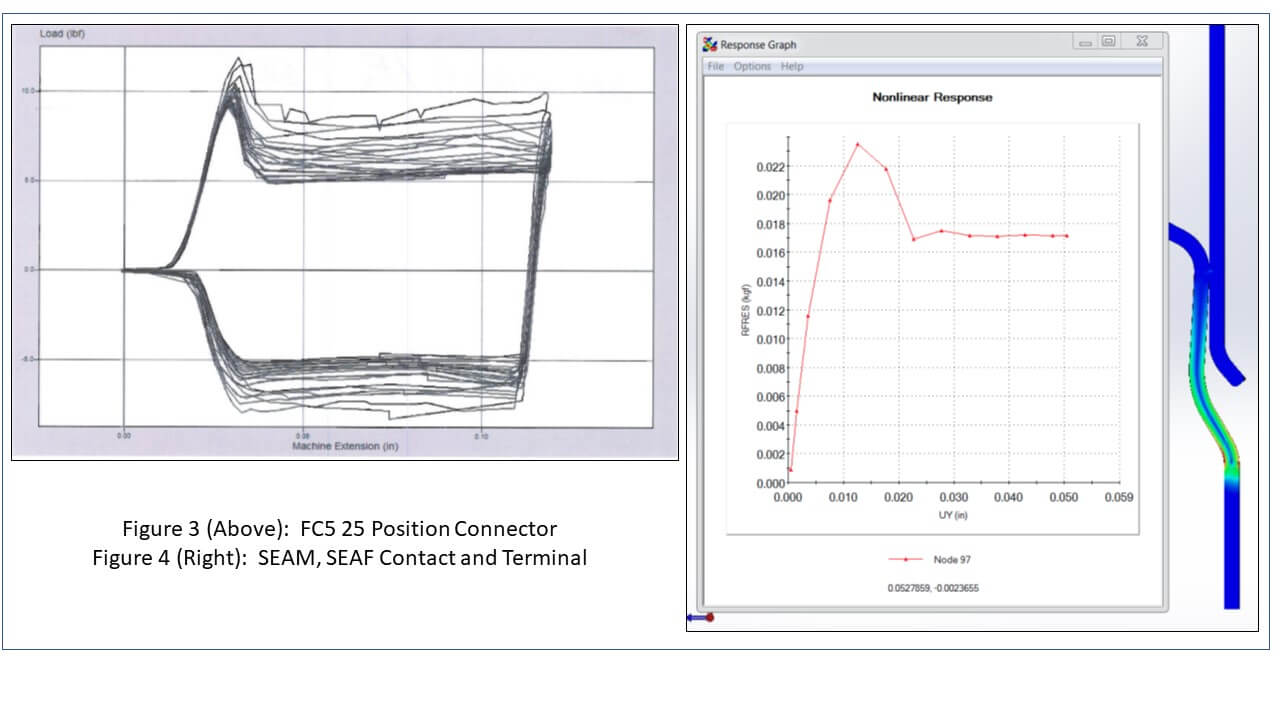
The mating force occurs in two stages, a spreading stage and a sliding stage (See figure 1 and 2). The spreading stage is a stage of higher force and responsible for the peak force (neglecting the bottoming out of the insulators). The insertion force is equal to the Y component of force of both the friction and normal force. During this stage there is friction plus the effects of spreading the contact open. The sliding stage is a stage of lower force in which only the friction force must be overcome as the normal force now acts in a perpendicular direction. There is no spreading effect in the unmating of connectors, which explains why it is generally more difficult to mate than unmate connectorsFigure 3 is the mating and un-mating plot, cycled 20 times, of a typical low pin count connector. It clearly displays the stages of mating at the connector level. This plot was generated during actual product qualification. Figure 4 is the FEA prediction for the mating cycle of a single circuit.
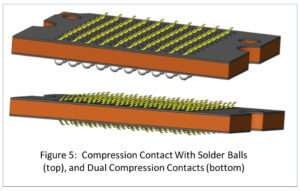
Calculating the mating and un-mating forces for grid array or pogo pin style connectors can be a bit trickier, especially if the connectors are stacked versus a side-by-side arrangement. These calculations often involve the calculation of springs in series or parallel. The resulting values can seem very counter intuitive and lead to over or under designed supporting hardware and systems. For example the mating force for the solder ball connector shown in Figure 5 is the same as the dual compression version of this connector even though there are twice as many springs.
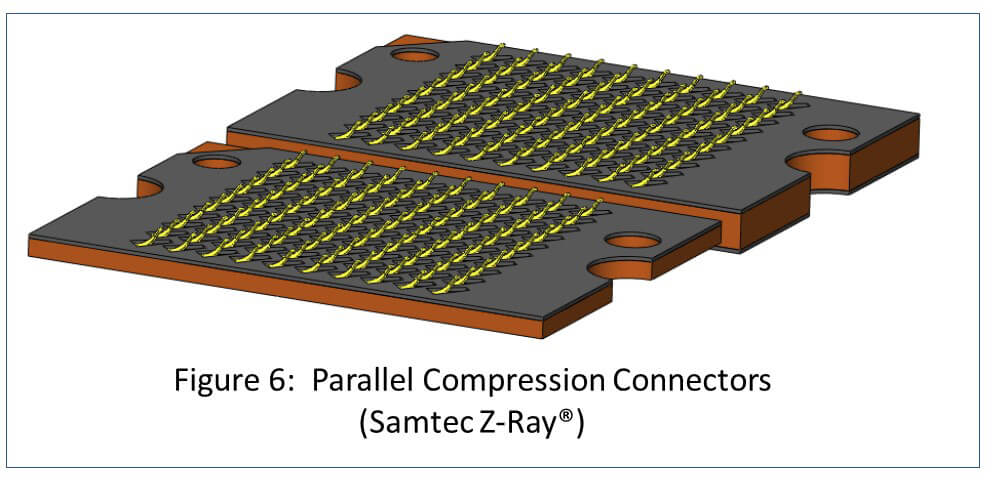
However, if you were to split this connector in half and placed each half side by side the force to mate and unmate it would double (see Figure 6).
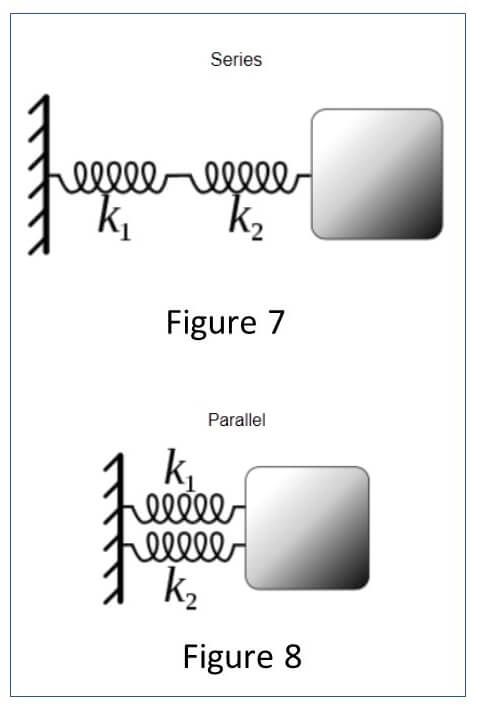
Here is why: the mechanical equivalent for a circuit of the dual compression connector shown in Figure 5 is shown in Figure 7.
In this case the spring constant k1 and k2 represent the spring rate of each beam. The resulting Spring rate is 1/Kequivalent = 1/k1 +1/k2. In our case both springs have the same rate k so 1/K equivalent = 1/k +1/k = 2/k => kequivalent = k/2, or half the spring rate of one spring. To fully compress each beam it is now necessary to double the displacement so you still end up with the same force.
The mechanical equivalent for a single circuit in the side by side single compression connector show in Figure 6 is shown in Figure 8. For this case kequivalent = k1 + k2. When k1 = k2, kequivalent= k + k =2k or twice the spring rate. You now generate twice the force for the same displacement.
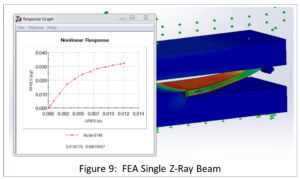
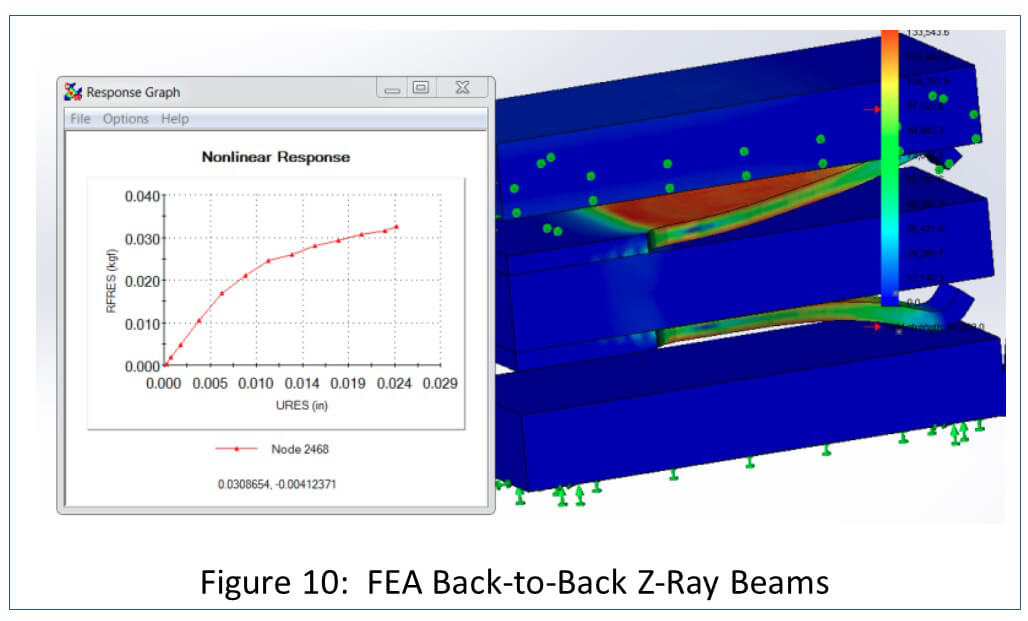
Figure 9 compares the FEA predictions for a single Z-Ray® beam (Z-Ray is a low profile, compression contact in an array format); Figure 10 compares back-to-back Z-Ray beams.
In this case the total mating force would be 31 grams times the number of ciruits in the connector. It does not matter that there are two springs in each circuit. The same calculations would apply to all Samtec dual compression connectors, like Z-Ray and GMI.
In conclusion the forces resulting from the mating and the unmating of electrical connectors are a function of contact geometry, contact normal force, friction and insulator binding or bottoming out.
Binding and bottoming out are to be avoided and controlled more by the user of connectors than the connector manufacturer. customers of Samtec connectors use this force data in the design of their system to deterime if inject/eject hardware is needed and of what size it should be. Samtec makes this data readily available to customers in the form of qualification test data taken for smallest, middle and largest position counts connectors. Values for position counts not directly qualified may be found by simple linear interpolation or they may be calculated directly by the methods outlined in this paper.